机械设计的基本原理9.16

Hertz Contact: Line Contact

赫兹接触：线接触

Consider a cylinder on a flat plane as shown. There appears to be a flat region where the cylinder and plane meet. What is the dimension δ required to obtain the observed width B? 

考虑如图平面上的圆柱体，看起来好像接触的区域有一部分是平的。那么得到尺寸宽度B需要的δ怎么计算呢？

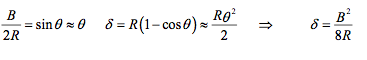
Could this δ be due to surface roughness factors? If B = 1.5 mm, R = 37.5 mm, and then δ = 7.5 μm, which seems small, but if smooth metal surfaces are used, δ is likely due to Hertz contact. Indeed, contact between two cylinders with parallel axes is a special case of Hertz contact stress theory ¹but it has been studied in great detail², especially given the fact that a cylinder in contact with a surface is far more rigid than a sphere in contact with the same surface³. Given two elastic cylinders of diameter d1 and d2 in contact over a length L, the rectangular contact area is of width 2b: 

δ是否因为粗糙度引起的？如果B = 1.5 mm, R = 37.5 mm，那么δ = 7.5 μm，看起来很小，但是采用的是光洁度很高的面，那么这个值可能是赫兹接触应力引起的。事实上，两个接触的圆柱体是赫兹接触应力理论的特殊例子，但是很多人已经给出了研究成果，尤其是与平面接触的刚圆柱度要比球体接触的刚度更大。已知圆柱体的尺寸d1和d2，接触长度为L，长方形接触区域的宽度为2b，那么：

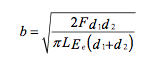
For a cylinder of diameter d1 compressed between two flat rigid surfaces (E2 is infinite), the displacement of the center of the cylinder relative to one of the surfaces is: 

对于直径为d1两面受刚性平面挤压的圆柱体，圆柱体中心相对于平面的位移为：

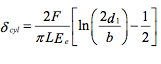
For an elastic cylinder on an elastic flat plate, this equation diverges, which is a peculiar result of the plane stress theory used. To determine the displacement of the center of a cylinder with respect to a point at distance do below the surface, a two-part solution is used. The first part is the displacement due to the deformation of the cylinder as given above. The second part is for the deformation of the elastic flat plate as a rigid cylinder is pressed into it, whereby Saint-Venant, a reasonable assumption is do = 3d1: 

对于弹性圆柱体接触弹性平面的情况，上面的公式会出错，因为我们采用了平面板件应力理论。为了计算接触面距离为d0的圆柱体位移，需要采用两个分量的计算方法。第一部分是因为上面的变形引起的。第二部分是平面被刚性圆柱体压入后产生的弹性变形，根据圣维南定理，合理假设do = 3d1：

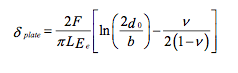
The deflection of the cylinder center with respect to a point three cylinder diameters below the surface is δcyl + δplate. The contact pressure is:

圆柱体中心相对于0.3mm以下平面的变形为δcyl + δplate.。接触应力为：

The maximum shear stress is 0.3q which occurs at a distance of 0.786b below the surface. This is why many failures seem to result in a delamination of material. The state of stress below the contact surface is given by: 

最大剪切力在低于平面0.786b处，其值为0.3q。这就是为什么很多失效看起来是因为表面材料脱落引起的。低于基础面以下的应力状态为：

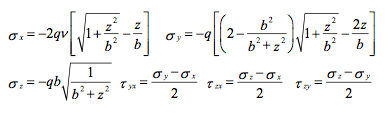
The spreadsheet Hertz_Line_Contact.xls can be used to easily evaluate these equations. In practise, it is very difficult to achieve line contact between surfaces with more than one cylinder at a time because the line contact is so rigid and deformations so small compared to surface flatness and misalignment errors. To prevent edge, loading barrel-shaped rollers are often used in applications such as roller bearings. 

计算表格Hertz_Line_Contact.xls可以用来方便我们评价其结果。实际上，圆柱体在两个平面之间的接触很难是线接触，因为线接触的刚度太大，其产生的变形还没有平面度和对齐误差大。为了防止锐边，通常采用桶状的滚子，例如滚动轴承。

It is wise to create a design where an object that was to make line contact instead has a very large major radius and thus makes point contact even when there is misalignment. Check your design and imagine how contacts change with misalignment. 

你可以设计一个采用线接触，但是曲率半径很大的形式，这样你就可以得到点接触，而且不受对齐误差的影响。检查你的设计，看看接触情况会怎么样随着对齐误差而发生变化。

1. See A. Slocum, Precision Machine Design, Society of Manufacturing Engineers, Dearborn, MI, 1996, pp 236-237
2. See J. Lubkin "Contact Problems," in Handbook of Engineering Mechanics, W. Flugge (ed.), McGraw-Hill Book Co., New York, 1962; and T. Harris, Rolling Bearing Analysis, John Wiley & Sons, Inc., New York, 1991.

3. This makes rolling cylinders extremely important machine elements; however, the stress concentra- tions associated with the edges of the cylinders requires them to be generously rounded.